Have you ever noticed that some proportions in woodworking designs seem to look better than others?
It may have something to do with what is known as the Golden Ratio, which equals 1.618 and is represented by the Greek letter "Phi" Φ.

Have you ever built something and thought it looked a little off-balance?
There's a secret weapon woodworkers use to create pleasing proportions: the Golden Ratio!
Golden Ratio Calculator
Enter a dimension:
Choose which dimension you are looking for:
The result is:
We will explain, in brief, what is the Fibonacci Sequence and how it is linked to the Golden Ratio, why we will use the ratio in more of our designs and how we use the Golden Ratio/ 1.618 when designing our woodworking projects.
You can learn more about the the discoveries of Leonardo Fibonacci by clicking here.
That said, it is not essential to use the golden rule when designing new projects.
However, it is said, that a high percentage of people do find that items designed using the golden ratio find those designs to be naturally more appealing to the eye.
Beauty is in the Eye of the Beholder. Margaret Wolfe Hungerford
Why use the Golden Ratio in our designs?
You may be asking if it is not essential to use the golden ratio in our furniture designs then why bother?
We feel that there is no denying the importance of using the golden ratio as it not only has been used in architectural design, going as far back as the pyramids but it's also found all around us in nature and space.

The Fibonacci sequence is prominent in the botanical realm that we feel it's only fitting that we use when building with wood.
We use Pine in many of our wood projects, so let's take the pine tree as an example to explain the Fibonacci sequence in nature.
To start we'll look at the Fibonacci sequence itself and how it is developed.
What is the Fibonacci Sequence or Golden Ratio?
It is actually a very basic sequence where the next number is found by adding the sum up to the previous number.
We start the sequence with the first two numbers we know of being "0" and add it to the next number "1", so 0+1=1, so now we have the beginning of the sequence being 0,1,1.
Now to calculate the next number in the sequence we add the sum to the preceding number from the current sequence (0,1,1) together, so 1+1=2, the sequence is now known as 0,1,1,2.
Once again, adding the sum with the preceding number from the last sequence, so 1+2=3, now we have 0,1,1,2,3.
Next we add 2+3=5, gives us 0,1,1,2,3,5... and so on.
Here is a table to give you a better idea.
The Fibonacci Sequence
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377...
0+1=1
1+1=2
1+2=3
2+3=5
3+5=8
5+8=13
8+13=21
13+21=34
21+34=55
34+55=89
55+89=144
89+144=233
144+233=377
233+377=610 and so on
The Fibonacci Ratio
As we get to the higher numbers and you divide the sum with the previous number you will get 1.618...
Examples:
377 / 233 = 1.618025751072961...
610 / 377= 1.618037135278515...
Now that we know how the sequence is developed we can start by looking for it in nature.
One way to find it is by creating what is called the Fibonacci Spiral.
Using the Fibonacci sequence starting with the number "1" in the sequence, whereas "0" can't represent anything, we start by drawing squares.
We have two number "1's" in the sequence so we start by drawing two squares that are 1 x 1.
Then the next number is a 2, so next to the two first squares we draw a square that is 2x2.
Next to those three squares, we draw another that is 5x5 and so on...
As we continue on you will create the Golden Rectangle that looks like the one below.

You can continue to build on this rectangle. Making it larger and larger with the numbers in the sequence but the rectangle will always maintain its golden ratio.
Interesting Fact: Look at the rectangle, then look at the shape of your computer or television monitor? Does it appear similar in any way? If you were to stretch the image of the rectangle to the edge of the screen, it would likely be very close to matching the Golden Rectangle ratio.

Now you may be wondering, How does this rectangle relate to a Pine Tree?
Easy, can't you see it?
No worries, it's not that evident at first but once we show you the next step you will have an OMG moment!
All you need to do now is start from the first 1x1 box you drew and start drawing a line with all the intersecting boxes as shown below. This will create what is called the Fibonacci Spiral ( We apologize the squares weren't drawn the same way as the image above but the ratio and outcome will always be the same.)
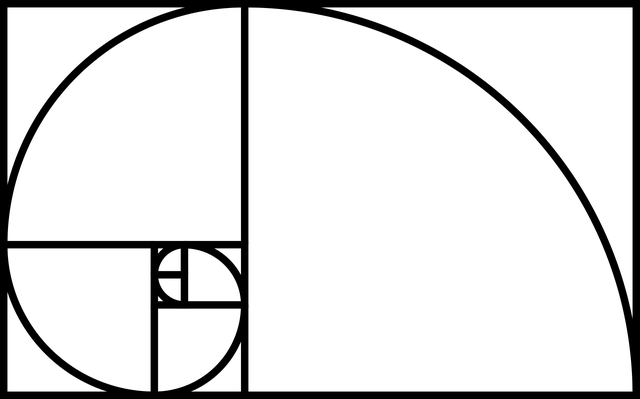
Don't worry, we're getting real close to correlating this with a Pine Tree.
Now that you see this spiral you will start seeing it everywhere in nature.
The first thing that comes to mind when looking at this spiral is the shape of a sea shell you've probably held up to your ear as a child to hear the ocean.

Now be an adult and slice that shell in half and you will see the Fibonacci Spiral that is created in nature.

Which now brings us to a Pine Tree or at least its cone. The spiral patterns as shown in the image below will match numbers in the Fibonacci Sequence. In the image below it shows that there are 8 spirals and if we were to count them in the opposite direction there will be 13.

Okay, so we're not using pine cones to build our wood projects so why would we use the ratio in our project designs?
Again, it comes down to proportions that most people find comfortable or pleasing to the eye.
Especially if you look at wood furniture like tables, dressers, drawers, and anything else that has rectangular shapes or proportions.
These proportions are ingrained from our day-to-day lives and it may not be apparent but it does influence how we perceive a product.
So as not to disturb the course of nature, we've decided to try and maintain the Golden Ratio within our projects as much as possible in both our woodworking and website design.
How We Use The Golden Ratio In Our Designs
Basically we either take the longest length of a project and divide it by the Golden Ratio 1.618 or take the shortest length and multiply it by 1.618.
Example: If we want a coffee table to be 42" for the longest length, we would divide that by 1.618 which equals 25.957972... Round it off to the closest 1/4" or 1/2" or so, we get 26", so the tabletop would be 42" x 26" which equals to the shape of the Golden Rectangle.
Now for the height of that table, we would take the shortest number, 26" and divide that by 1.618 which equals 16". You guessed it, that is within a standard height for a coffee table, most being between 16" to 18" in height.
We do round off the measurements within 1/4" or 1/2" to make it easier for building but the overall impression is still pleasing to the eye.
Here is an example with furniture we recently built

Another way is by using a tool that will automatically give you the 1.618 ratios.
I could draw up some plans but I found a great tool also known as the golden mean caliper on Amazon by clicking here.
With this tool, you can start to draw plans up on paper and then figure out the proportions quickly.
It's also fun to check items around the house, in nature or even the bones on your body that all seem to follow this ratio.
The Golden Ratio In Furniture and Woodworking Design!
We hope you found this information about the golden ratio in woodworking to be interesting and help you be little more aware about the patterns in nature all around us.
Did you know about this golden rule before? Are you able to find the golden ratio in your surroundings?
Let us know by leaving a comment below. We would love to hear from you.
Cheers
Paul

I am no expert in this, but as I go thru, I do notice that you have a lot of knowledge on it. I have a better idea of the calculation and the formulation of it all. I feel you have the authority in this niche. Your experience will definitely benefit someone who is looking into this topic. As I said, I am no expert, but I definitely learned something today.
Cheers
It may look and sound somewhat complicated at first but once you start using it and observing it in day to day life it really becomes much easier.
Thank you for visiting and I wish you well.
Cheers
Paul
This is an awesome article, though I must say some of it went over my head! I was never much of a numbers man, though. That being said, I love how you have taken art and mixed it together with science. This is beautiful, and it’s pretty amazing. I’m glad you made this post because it’s so cool to see something like this come alive in a scientific but beautifully artsy way!
You would be surprised how much this rule is used in art. You can Google “Fibonacci Mona Lisa” for instance and you will see how that painting and so many works of art use the Fibonacci Sequence.
Cheers
Paul
What an insightful article! The Golden Ratio! I never knew (and my father is a carpenter / woodworker)! I’m going to have to run this by the man himself and see what he knows of it! Fun trivia!
Admittedly, I never had heard of the Golden Ratio. You did a fantastic job explaining it! I appreciated the drawings and the examples you used to get to why and how you use it in your own woodworking. I find it absolutely phenomenal and as you say, it’s all around us! I learned something today! Thank you so much for sharing your wisdom in such a brilliant way!
It was an incredible revelation to us as well when we first learned about it.
Once you see it, you can’t unsee it!
Please share it with your family and friends.
Have fun with it.
Cheers
Paul
Very interesting concept, I had never heard of the Fibonacci Sequence of the Golden Ratio before reading your post. Amazing how often it comes up in our normal lives and not even knowing it! I will definitely be looking for this now when I am out and about. Thank you for teaching me about this!
It’s one of those things that exists yet many are not aware of it. Schools seem to skip this type of information. They will give you the ratio to do calculations like Pi or this one Phi but never get into the reasoning why that ratio exists.
Have fun 😉
Paul
Hey, Your article is very awesome for everyone. While doing Google “Fibonacci Mona Lisa” for instance we will see that painting and so many other works of art that use the Fibonacci Sequence. Your explanation is awesome for me. I appreciated the drawings and the examples you used to understand why and how you use the golden rule in your own woodworking. I learned a new thing today. Keep it up.
We are always pleased to hear when someone learned something new from one of our articles. I hope you bookmarked this page as we will continue to present new projects and resources.
Simply amazing. I see what you did there, Paul and Brenda. Disguising a mathematics lesson as a woodwork/design post – very clever. We humans certainly create our best work when inspired by Nature, although being able to distill all that natural mystery down to a mathematical formula sometimes takes all the fun out of it. Definitely bookmarking this site for future reference…and maths lessons!
Thank you for sharing.
Hehehe…one can be fooled into liking math. 😉 Thanks for following us. Our goal is to continue inspiring people to consider starting their own side business, whether it be woodworking or any other business niche you are passionate about. Cheers
Hey, I enjoyed reading your guide on the Golden Ratio in Woodworking. I am not an expert. While reading, I found many useful facts. Using the Fibonacci sequence starting with the number “1” in the sequence, whereas “0” can’t represent anything, we start by drawing squares. While searching on google I know that it is used in painting and many artworks also. Thank you for teaching me about this!
It’s amazing to see how one can take those numbers then represent them by squares which in turn create the spirals. I tried to explain as easily as possible with the limited knowledge I have on this subject. Our goal was to show how we use it in woodworking but one can’t only say we use that golden rule without explaining its origin.
Many thanks to you for giving us such a wonderful article. I’ve never heard of the Fibonacci sequence or the Golden Ratio before reading your article. A great article my father is a woodworker so I heard about this golden ratio and have used it in some of my woodworking. You really deserve a lot of compliments and a lot of great work for your article so well presented. I found it difficult at first, but later realized it was very easy.Through it, all the woodwork has been really fascinating and has got beautiful shapes. When I’m out I will definitely look for these more because I love them and I learned these and want to learn more and thanks so much for learning so much through your article.
I like this article a lot and soon I will experience it in real life and share my new discoveries with you.
We would love to hear and see what you have discovered. Once I learned about the rule it became evident in so many areas. Even today I learned that it is also being used to predict the stock market. I can’t wait to see where else the golden rule is being used.
Very interesting! I’ve learned about the Fibonacci sequence many years ago because it is also a tool that is used in the stock market. I’d love to explain how it works but it would take up too much space and time but in a nutshell, Fibonacci sequence are horizontal lines on a stock chart and is used to “predict” where a stock price would probably peak or bottom. Since many traders use this tool, it tends to be self-fulfilling. Fibonacci spirals are also used. Thanks for sharing your post, I learned something new today
Sunny
Amazing! I know that the Fibonacci sequence was used in art, architecture, woodworking, and other fields but never thought about the stock market. You’ve thought me something new and now need to check that out for myself. It really makes one wonder if we are truly within a simulator. 😉
Hiya Paul
I had heard of the Fibonacci sequence but I didn’t know what it was until I read your article about the Golden Ratio. Thank you for performing the near miracle that is teaching me something involving numbers in a way I could actually understand!
Your visuals worked really well for me and I will be able to point out the Golden Ratio and Fibonacci sequence in nature to my cubs which will be great. The first thing I’m going to do at the weekend is find a pine cone and show my cubs the pattern.
Thank you for teaching me something new that I can share with my family, krs PurpleLioness
It’s amazing how we start seeing things differently once we learn something that has been in front of us our whole lives. Have fun observing this weekend. The golden ratio also helps us when trying to develop new projects. Sometimes when drawing up a new design for furniture something doesn’t seem right I’ll start using the ratio and adjust dimensions accordingly and before we know it the design with the new dimensions based on the golden rule looks great.
The way you have used the pictures to illustrate your point about the Golden ratio for woodworking made it a lot easier to grasp the concept. It was totally beyond me in the beginning. I certainly learned a lot and I can see this will be helpful to a great many people.
Thank you, Lisa,
I am a visual person so when explaining something I know how helpful it is to have images.
Cheers
Paul
Enjoyed this. Fibonnaci Bodine, in wonderment animation, is what I said to my calculus instructor, out loud in class, when he went over this. I had forgotten the golden number, the golden ratio and Fibonnaci. Newton took over once we got into the mechanics of motion.
Thanks for the refresher and when in engineering school I found many things in higher mathematics that seemed Jethroesque.
This is a very good post with interesting and useful information. I, myself, am working on an art project to produce artwork on an item constiting of increasing redis spirals and you have given me the math again. I am sure readers will find this sort of information of interest and the guys and girls at google who send out the robotic readers will like this.
Thank you again. Have fun with it. CQ.
Thank you,
I am no mathematician, scientist, or artist but I can’t deny my interest in this subject. I may not be the best instructor in this subject but wanted to share this interesting phenomenon with others to help spark awareness. I’ve only touched on a very small aspect of this subject in a similar style as telling someone here is a computer, you can type words on it without diving into how much more a computer can do and how complicated it really is. Best of luck with your art project with Redis Spirals. I would love to see your creation.
Cheers
Paul
Over the years I’ve read a lot of material in physics, esotericism, space, the Pyramids, and a lot of other intersting and sometimes controversial stuff. I remember reading a few books, which I can’t recall at the moment, but they referred to the Golden Ratio. If I’m not mistaken, even our elbo to wrist and other joint relationships reflect this ratio. I’m no expert in this area, and in fact, I feel lost with some of it. But I know that the Golden Ratio pattern is seen in galaxies, hurricanes, and even DNA molecules (obviously on a micrfoscopic lervel), and those are just a few examples as we go from macro to micro. It seems to be everywhere. I would guess that we would be blown away at how many things, if not everything in one way or another, have a direct mathematical connection with this formula. The one thing that just occurred to me is how the snowflake has six sides, spikes or whatever you call them. Without even researching this, I’m confident that although the number 6 isn’t in the sums of the Fibonacci Ratio, the overall dimensions of the snowflake will reflect this principle, similar to the petals on a flower. Any thoughts on that?
Thanks for an interesting article.!
Darrin
Hey Darrin,
Thank you for visiting my site and your interest in the golden ratio. I myself am not a mathematician or scientist but like you are very intrigued by this golden ratio developed from the Fibonacci sequence. It can’t believe it is a coincidence that so many things surrounding us are somehow linked to this sequence. You are correct in regard to the ratios comparing the bones and shapes of different parts of our body that are correlated to that ratio. It is found in both the micro and macro environments. I believe that if other things like the snowflake don’t follow the Fibonacci sequence then it may be following another rule or ratio that we may not yet be aware of. “Nature” as we call it follows a strict set of rules in order to be created and grow. Although evolution causes organic matter to change shapes and behaviors it all still follows the basic golden ratio. I’ll end my comment here as this subject can delve deep into conversations about our creator and maybe best discussed on a different platform.
Thanks
Paul
Very well explained and presented. (Thank you).
How about showing us how to make a side/coffee table using the golden ratio and neo classical design for the frame and incorporating Penrose tiling in different timbers for the top.Looking forward to the result. – Arthur
I do like the idea of building a side or coffee table using only the golden rule for all the dimensions. We’re not really into the neo classical design for the frame but do like the idea of incorporating a Penrose tiling design for the top. I do like the look of the P1 tiling using Penrose’s original set of six prototiles. I could use various types of wood to accentuate the six different prototiles so stay tuned as we get around to that in the near future.
Very intruiging topic, will read up more about this, great article Paul!
It is quite intriguing and there are so many other natural laws that are just as intriguing. I hope to touch on those in future posts.
Thank you for the explanation. In the example of coffee table how much should be the height. 48" x 26" x Height?
Thanks, the height should at a functional height when seated. Approx 18″ to 19″. There is little advantage to use the Golden Ratio for the height, it would be different if you are facing the long part vs the shorter end of the table.
Very helpful